Table of contents
수익률과 기하평균
직접 투자를 하다 보니, 내가 과연 1년에 얼마나 수익을 내는 것인지 확인을 해볼 필요성을 느끼게 되었습니다. 지금은 현재 매월 1회 현재 수익률 정도만 캡처해서, 그 추이만 살펴보고 있는 중인데요. 다양한 방식으로 수익률을 확인해보고, 더 나아가서 시장지수와 비교하여 어떻게 움직이는지 확인해보고자 합니다.

그전에 오늘은 연평균 성장률(compound annual growth rate, CAGR)에 대해서 공부한 내용을 정리해보려고 합니다. 특히, CAGR을 계산하기 위해서 사용되는 개념인 기하평균(geometric mean)에 대해서도 같이 정리해보겠습니다.
수익률을 계산해보자
우리는 평균에 대해서 매우 잘 알고 있습니다. 그리고 흔히 평균이라고 하면, "산술평균"을 떠올리게 됩니다. 그럼 산술평균은 무엇일까요? 예를 들어서 설명하겠습니다. 아래와 같이, 철수가 5년 동안 투자한 성과가 나와있습니다.
| 0년차(투자시작) | 1년차 | 2년차 | 3년차 | 4년차 | 5년차 | |
| 수익률 | 0% | 2% | 3% | 4% | 2% | 4% |
| 수익금 | 0원 | 20,000원 | 30,600원 | 42,024원 | 21,582원 | 44,597원 |
| 원금+수익금 | 1,000,000원 | 1,020,000원 | 1,050,600원 | 1,092,624원 | 1,114,476원 | 1,159,055원 |
매년 수익금은 재투자 된다는 가정하에 계산하면 위와 같습니다. 위 결과에 대해서 아래와 같이 두 가지 질문을 해봅시다.
1. 연 평균 얼마를 벌었는가?
간단히 산술평균을 사용하면 됩니다. "수익금" 열에 있는 모든 금액을 더한 후, 5로 나누게 되면 약 31,811원, 즉 1년에 대략 3만 원씩 수익을 올렸다고 볼 수 있습니다.
(20,000원 + 30,600원 + 42,024원 + 21,582원 + 44,597원) / 5 = 31,811원
2. 연 평균 얼마의 수익률을 얻었는가?
실은 요 질문에 대한 답을 구하려고, 이 글을 적고 있습니다. 위와 마찬가지로 산술평균을 사용하여 "수익률"열에 있는 모든 수익률의 평균을 구하면 될까요?
(2% + 3% + 4% + 2% + 4%) / 5 = 3%
3%가 나오네요. 수익금이 16만 원 좀 안되는데, 1년에 3%씩 5년 해서 대략 15만 원 정도 벌었다고 생각하면 거의 맞다고도 볼 수 있을 것입니다. 하지만 수익률에 대해서 이렇게 계산하면 오차가 있을 수 있는데요, 영희의 투자 결과를 한번 살펴보시죠.
| 0년차(투자시작) | 1년차 | 2년차 | 3년차 | 4년차 | |
| 수익률 | 0% | 100% | -50% | 100% | -50% |
| 수익금 | 0원 | 1,000,000원 | -1,000,000원 | 1,000,000원 | -1,000,000원 |
| 원금+수익금 | 1,000,000원 | 2,000,000원 | 1,000,000원 | 2,000,000원 | 1,000,000원 |
예제를 통해서 오차가 있다는 것을 설명하고 싶어서, 조금 극단적으로 변동성이 있는 투자 결과를 예로 들어보았습니다. 영희는 4년동안 100%의 수익과 -50%의 수익을 번갈아서 올렸고, 투자가 끝난 시점에는 원금과 동일한 결과가 나왔습니다. 내 포트폴리오가 연평균 얼마나 벌었는지 산술평균을 이용하여 동일하게 계산해보겠습니다.
(100% + (-50%) + 100% + (-50%)) / 4 = 25%
연평균 25% 수익을 올렸다면, 4년동안 100%, 즉, 원금의 두배가 되어야 맞습니다. 하지만 실제로 등락을 반복하여 원금만 남아 있으므로 실제로 이 포트폴리오의 경우, 연평균 수익률은 0%가 되어야 맞을 것입니다. 그렇다면 내 포트폴리오가 연평균 몇% 의 성장을 했는지 계산을 하려면 어떻게 해야 할까요? 바로 기하평균을 이용하여 계산을 해야 됩니다. 계속해서 설명해보겠습니다.
기하평균(geometric mean)이란?
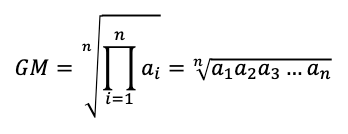
평균을 구하려는 모든 수를 곱한 다음, 이 수에 수의 개수만큼 n제곱근을 수행해주면 됩니다. 기하학적 의미를 살펴보면, 가로의 길이가 a이고, 세로의 길이가 b인 직사각형이 있다고 했을 때, 이 직사각형의 넓이와 같은 정사각형을 구했다고 해봅시다. 이때, 이 정사각형의 한 변의 길이가 바로 기하평균으로 계산된 값이 됩니다.
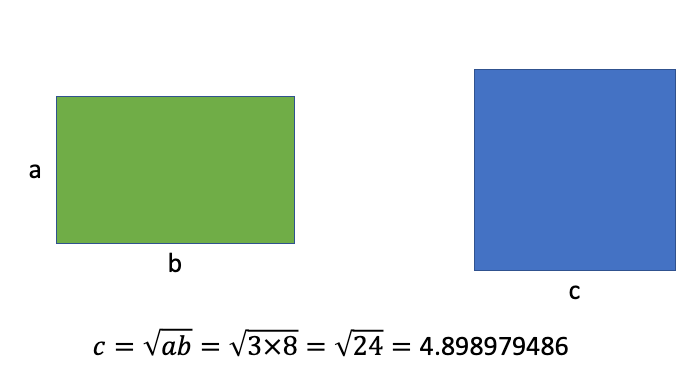
초록색 직사각형의 넓이와 같은 파란색 정사각형이 있다고 했을 때, 이 파란색 정사각형의 한 변의 길이를 바로 기하평균식을 이용하여 계산해볼 수 있습니다. 실제로 4.89를 제곱해보면 23.9xx가 나오는데, 거의 24에 근접하다고 할 수 있습니다.
기하평균의 의미?
그렇다면 이게 무슨 의미일까요?
의미를 알아보기전에, 평균을 왜 사용하는지 생각해보죠. 우리는 평균값을 사용하는 가장 큰 이유는 바로 비교하기 위함이라고 생각합니다. 어떤 학교의 반별 영어나 수학 성적을 비교해보고 싶을 때, 흔히 해당 반의 평균을 구해서 비교를 해보게 됩니다. 기하평균에서도 마찬가지로 비교를 해보기 위해서 사용되는 하나의 평균값입니다.
비교대상이 되는 값은, 수익률입니다. 철수의 투자예제를 다시 한번 살펴보겠습니다.
연차별 수익률에 1을 더한 후, 모두 곱해보겠습니다.
(1+2%) * (1+3%) * (1+4%) * (1+2%) * (1+4%) = 1.02 * 1.03 * 1.04 * 0.02 * 1.04 = 1.159055539
1을 더한 이유는 수익금에 원금까지 포함하기 위해서이며, 0보다 작은 수는 곱해질수록 계속 작아지기 때문에, 실제 올바른 계산을 위해서는 1을 더해줘야 합니다. 마이너스 수익률인 경우 1을 더하게 되는 경우 0보다 작은 값이 되므로, 실제로 원금에 곱해졌을 때 금액이 줄어드는 형태로 계산이 되게 됩니다.
어쨌든, 위와 같이 1.159055가 나왔는데, 여기에 원금인 1,000,000원을 곱하면, 1,159,055원이 나옵니다. 5년차에서 만들어진 최종 수익과 같은 값이죠. 1.159055에서 1을 빼면, 0.159055 즉, 5년 동안 15.9%의 수익을 올렸다고 해석할 수 있습니다. 또한 이렇게 5개의 숫자가 곱해졌는데, 이런 숫자들의 평균을 우리는 기하평균을 이용하여 계산해볼 수 있는 것입니다.
기하평균의 정의에 따라 5개의 숫자를 모두 곱한 뒤, 5 제곱근을 구하면 됩니다. 바로 이 내용이 다음절에서 설명드릴 연평균 성장률(CAGR, compound annual growth rate)의 기초가 됩니다.
연평균 성장률(CAGR, compound annual growth rate)
위에서 던진 두가지 질문 중, 두 번째 질문인 "연평균 얼마의 수익률을 얻었는가?"에 대한 답을 구하는 식입니다.

투자 시작 전 금액을, 평가 시점의 금액으로 나누면 얼마를 벌었는지 그 비율이 나오게 됩니다. 이것은 5년간 각각 수익률에 1을 더한 후 곱한 값과 같게 됩니다. 여기에 투자기간만큼 제곱근을 해주고, 최종 1을 빼주면 연평균 얼마만큼의 성장(수익)이 일어났는지 그 값을 알 수 있게 됩니다. 최종적으로 철수의 포트폴리오를 대상으로 CAGR을 구해보면 다음과 같습니다.
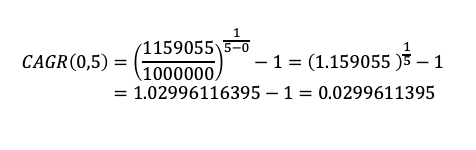
5년 동안 약 15.9%의 수익을 올렸고, 연평균 2.9%의 수익률을 기록했다고 볼 수 있겠습니다.
마치며
포트폴리오에서 현재까지 수익률은 쉽게 계산할 수 있지만, 투자 기간이 늘어남에 따라 과연 1년에 몇% 씩 내 자산이 성장하는지 그 값을 알고 싶을 때 사용하는 지표인 CAGR에 대해서 알아보았습니다.
기하평균의 정의를 투자에 빗대어 한번 더 곱씹어보자면, 투자기간이 2년이라고 하면, 1년차, 2년 차 각각의 수익률에 1을 더한 후 곱했다는 것은 그 직사각형의 넓이를 이야기합니다. 즉, 직사각형의 넓이는 2년 동안 올린 총수익률을 나타냅니다. 원금을 곱하게 되면 수익금이 되겠지요.
여기에 제곱근(2년이므로..)을 취하면, 바로 넓이가 같은 정사각형의 한변의 길이가 나옵니다. 요게 기하평균의 정이지요? 결국 수익률은 변함이 없고(넓이가 같으므로..) 정사각형의 한 변의 길이로 그 평균값을 알려줌으로, 우리는 이 값을 이용해서 정량적으로 1년에 얼마씩 성장했는지 가늠할 수 있게 되는 것입니다.
사람은 머리속에 3차원까지 그릴 수 있으므로, 3년 동안 투자를 했다고 하면, 아마도 모두 곱했으니 직육면체의 부피가 될 것이고, 세제곱근을 해버리면, 정육면체 중 한 변의 길이가 나올 것입니다. 4년, 5년, 차원이 늘어나지만 기하학적으로 동일한 의미를 지닐 것이므로, 우리는 투자기간에 따라 정량적으로 1년에 몇 % 씩 성장했는지 알 수 있을 것입니다.
제 직관적으로 생각하고 이해한내용을 정리하고, 또 공유해보았습니다. 수학적으로 의미가 타당한지는 잘 모르겠지만 혹시나 부족하거나 잘못된 내용이 있으면 언제든 댓글로 피드백 부탁드리겠습니다. 고맙습니다.
'투자 공부 > 기초' 카테고리의 다른 글
| 장기투자의 적! - 변동성 (0) | 2021.03.14 |
|---|---|
| 변동성과 표준편차 (0) | 2021.03.12 |
| 제로금리와 미국 장기채권 (0) | 2021.03.01 |
| 액면 분할(stock split) 알아보기 (0) | 2021.02.26 |
| 주식/채권 자산 배분 (0) | 2021.01.25 |