채권의 가격 계산
이전 포스팅에서는 미래에 내가 얻을 수 있는 자산을 현재 시점으로 가져와서(?) 계산하는 방법에 대해서 알아보았습니다. 이때 할인율이라는 개념을 사용하였는데요, 5년 후의 100만 원이 5%의 할인율을 적용했을 때 과연 현재 가격으로 얼마인지 계산해보고, 현재 가치로 생각해보는 것을 학습하였습니다.
이제 지난번 공부한 내용을 채권에 적용해보려고 합니다. 채권은 기초에서 알려드렸듯, 발행 시 이미 얻을 수 있는 모든 자산이 다 정해져 있다고 하였습니다. 그리고 채권도 주식처럼 자유롭게 거래를 할 수 있다고 하였는데요, 거래를 하려면 현재 이 채권이 얼마인지 그 적정 가격을 알아야 할 것입니다.

지난 포스팅에서 배운 내용을 기초로 하여, 채권이 가진 현금흐름을 현재가치로 변환해보는 방법에 대해서 알아보겠습니다.
채권의 현금 흐름
채권은 발행 시, 액면가, 만기, 표면금리 이렇게 세 가지 요소가 반영되어 발행이 됩니다. 또한 만기때까지 정해진 현금흐름이 확정되는 특성이 있습니다. 예를 들 때에는 만기 때까지 고정적이 이자를 지급하는 이표채에 한해서 다뤄보겠습니다.
예를 들어, 액면가 1,000,000원, 표면이자율 5%, 그리고 5년 만기를 갖는 채권의 경우, 이 채권을 매수한 투자자는 다음과 같은 현금흐름을 갖게 됩니다.
| 0년 | 1년 | 2년 | 3년 | 4년 | 5년 | |
| 수입 | 50,000원 | 50,000원 | 50,000원 | 50,000원 | 1,050,000원 | |
| 지출 | -1,000,000원 |
첫해는 매수에 1,000,000원을 사용하였고, 이후 1년마다 50,000원의 이자를 받습니다. 그리고 만기때는 이자와 함께 원금을 받게 됩니다.
이런 현금흐름을 가지는 채권은 과연 현재가치로 얼마나 하는지 한번 알아보겠습니다.
채권의 현재가격
미래가치를 현재가치로 변환할 때에는 이자율(할인율)을 사용하였습니다. 마찬가지로 채권도 채권의 현재 가격을 구하기 위해서는 동일하게 이자율이 주어져야 합니다. 이때 이자율은 시장이자율이 됩니다. 표면이자율과 혼동하실 수 있는데 절대 혼동하시면 안 됩니다.
시시각각 변하는 시장이자율을 가지고, 현재 채권의 가격을 계산해보겠습니다. 우선 계산하기 전에 살펴보면, 매년 발생하는 현금흐름을 모두 현재가치로 변환한 후 모두 더하는 방식으로 계산을 하게 됩니다. 즉, 첫해 발생하는 이자인 50,000원에 대해서 현재 가치로 변환하는 공식을 적용합니다. 이후 2년 뒤 발생하는 이자, 3년 뒤 발생하는 이자... 그리고 만기 때 발생하는 이자와 원금에 대해서도 똑같이 계산을 하게 됩니다.
실제 계산을 해보려면 아래와 같은 공식을 사용하면 됩니다.
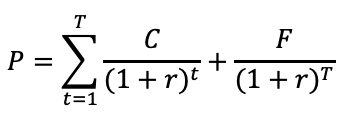
P는 채권의 현재 가격이고, T는 만기입니다. C는 이자로서 액면가에 표면이자율을 곱해서 나오게 됩니다. r은 시장이자율이고, F는 액면가(원금)입니다.
case 1 : r=0.02 인 경우

case 2: r=0.05 인 경우
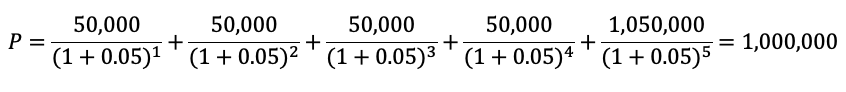
case 3: r=0.07 인 경우
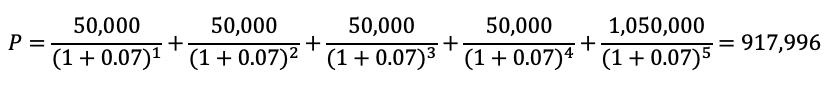
어떠신가요? 매년 발생하는 이자 50,000원은 모두 변함이 없습니다. 단 시장 이자율이 오르고, 내릴 때마다 채권 가격이 오르고 내리는 것을 알 수 있습니다. 시장이자율과 표면이자율이 0.05로 같은 경우 채권의 가격은 액면가와 같아짐을 확인할 수 있습니다.
위에 예로든 액면가 1,000,000원짜리 채권은 시장 이자율이 변동됨에 따라, 더 비싸게 혹은 더 싸게 가격이 계산됨을 알 수 있습니다.
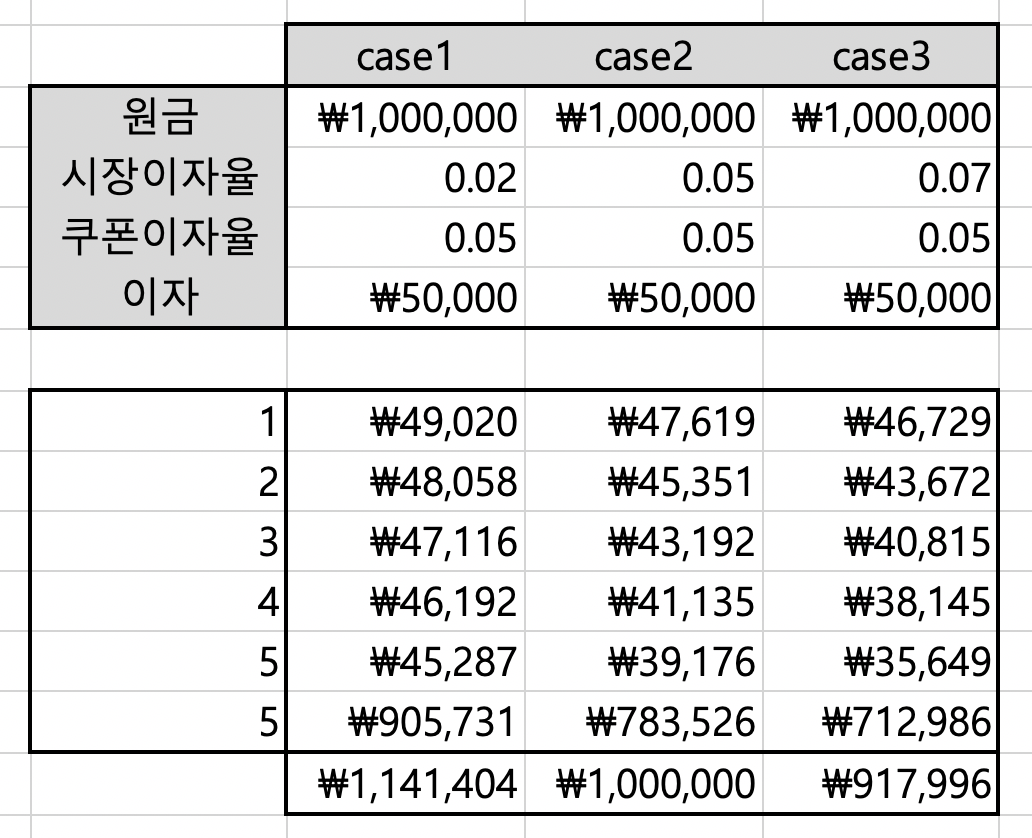
아래는 실제 엑셀을 이용해서 계산해본 과정입니다.
채권의 가격과 시장이자율과의 관계
채권은 발행할 때, 표면금리가 정해집니다. 이후에 유통시장에서 거래될 때의 채권 가격은 시장이자율에 따라서 그 가격이 변하게 된다는 것을 위에 계산식에서 알아볼 수 있었습니다. 그렇다면 채권의 가격은 시장이자율과 어떤 관계가 있는지 한번 살펴보겠습니다. (눈치채셨겠지만, 역의 관계(반비례)가 있음을 알 수 있으시죠?)
| 시장이자율 | 채권가격 | |
| case1 | 0.02 | 1,141,404 |
| case2 | 0.05 | 1,000,000 |
| case3 | 0.07 | 917,996 |
시장이자율이 오를수록 채권 가격은 내려가고, 반대로 시장이자율이 내릴 수록 채권가격이 올라갑니다. 수식으로 봐도, r이 분모에 위치함으로 채권가격 P와는 반비례관계임을 알 수 있겠네요.
위에 예로든 1,000,000원짜리 채권을 발행할 당시에 시장이자율이 5%라서, 5% 정도로 발행을 하였는데, 이후 시장 이자율이 오르는 경우에는 굳이 5%로 발행된 채권을 살 이유가 없을 것입니다.
그냥 은행에만 맡겨도 7%의 이자를 받을 수 있는데, 굳이 채권을 살 필요가 없는 거죠. 하지만, 이 채권을 가지고 있는 투자자가 돈이 필요해서 반드시 채권을 팔 수밖에 없는 상황이 돈다면 본인이 샀던 가격보다는 좀 낮춰서 팔아야 할 것입니다. 그래서 현재 시장금리가 7%로 올랐다면, 약 8~9만 원 정도 손해를 보고 이 가격에 매도를 해야 할 것입니다.
반대로, 시장금리가 2%로 떨어진 경우에는 5%의 표면금리고 발행된 채권은 투자가치가 올라갈 것입니다. 예를 들어 현재 예금금리가 2%인데, 4%인 특판상품이 나왔다고 해보죠. 그럼 사람들이 너나 할 것 없이 몰려서 가입을 하려고 할 것입니다. 즉 수요가 높아진다는 이야기지요. 채권도 마찬가지입니다. 수요가 몰리니까 가격이 올라가는 것이고, 그만큼 시장에서 가치가 올라갔다고 볼 수 있겠네요.
실제로 계산해봐도, 1,000,000 원주고 산 채권은 금리가 2%로 떨어지자, 14만 원 정도 그 가치가 올라간 것으로 계산이 되고 있습니다.
마치며
오늘은 현재 시장이자율을 알고 있을 때, 미래에 발생하는 현금흐름을 가진 채권의 가격을 계산해보는 방법을 공유하였습니다. 가장 중요한 두 가지 정도 리마인드 해보자면 아래와 같습니다.
1. 시장이자율과 표면이자율은 서로 다르다. (수식에서 r은 표면이자율이 아닌 시장이자율)
2. 채권 가격과 시장이자율은 서로 반비례(역의 관계)한다.
제가 가지고 있는 모든 포트폴리오에서 채권은 모두 파란불입니다. 위 계산대로라면 금리가 더 이상 내릴 여지가 없는 상황에서 매수한 채권은 더이상 오를 여지도 없어 보이는데요, 이번 공부를 통해서 채권 가격의 움직임을 조금이나마 알 수 있는 계기가 되었습니다.
'투자 공부 > 채권' 카테고리의 다른 글
| 제로 쿠폰 채권(Zero coupon bond) (2) | 2021.02.17 |
|---|---|
| 듀레이션(duration) (0) | 2021.02.14 |
| 만기 수익률(Yield to Maturity) (0) | 2021.02.12 |
| 현재가치 / 미래가치 계산 (1) | 2021.02.05 |
| 채권 기초 (0) | 2021.02.03 |